I’ve built a straightforward capture system in emacs for storing links in a designated file. Lately, however, I’ve ventured into the world of Obsidian, a note-taking application, to explore its capabilities.
To make link capturing effortless, I initially experimented with Instapaper. The ease of capturing web content with Instapaper is genuinely remarkable—simply click a button in your browser, and voila, the content is saved for offline reading. It’s equally efficient on an iPad; just share a link with Instapaper, and it’s saved. But despite this convenience, I prefer not to rely on third-party apps and sought to create a similar workflow within Obsidian.
Objective
Capture web links efficiently and store them in an Obsidian vault. The collected links will be treated as a “reading list” and appended to a specific Obsidian file. Be as distraction-free as possible.
Implementation
To create a new note in Obsidian, you can do the following:
obsidian://new?vault=name&filepath=Reading%20List/Untitled.md&content=content
This approach is too clunky, it requires URL encoding, making sure content parameter is constructed properly. Too much work.
Using AppleScript, we can begin by verifying if the file already exists:
set obsidianFilePath to POSIX file "Valut/Reading List.md"
tell application "Finder"
set fileExists to exists file obsidianFilePath
end tell
If it does, appending new content is straightforward:
set fileDescriptor to open for access file obsidianFilePath with write permission
write obsidianContent to fileDescriptor starting at eof
close access fileDescriptor
To know if the capture was successful or not, create a system notification:
display notification "Item captured in Obsidian" with title "Quick Capture - Obsidian"
And the most important thing: get the current safari tab’s URL and title:
tell application "Safari"
set currentURL to URL of current tab of window 1
set currentTitle to name of current tab of window 1
end tell
Equipped with these, we can write a complete script that:
- Fetches current tab’s URL and title
- Sets up appropriate content to be written
- Checks if the file exists
- Writes to the file
- Generates notification for success & error
Automation
In Apple Automator, we create a new “Quick Action” and select “Run AppleScript”:
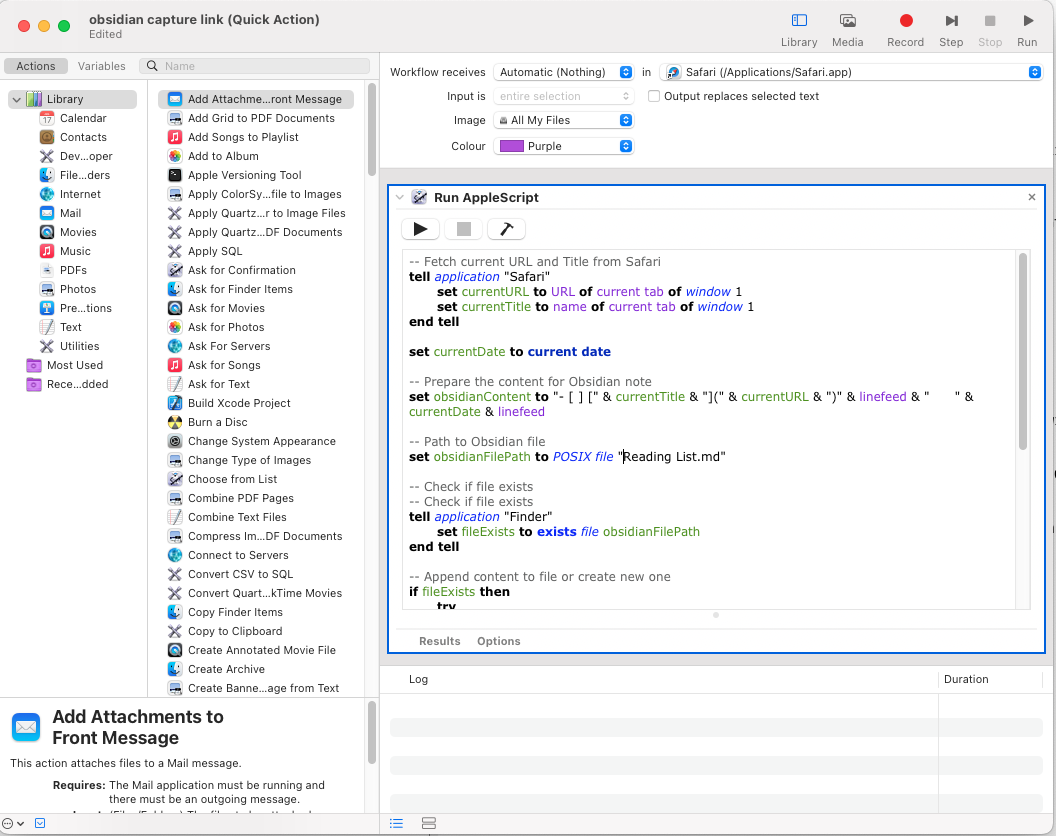
To make this process even more effortless, associate this Automator action with a keyboard shortcut. Navigate to System Settings → Keyboard → Shortcuts → General, find the Automator Quick Action you’ve saved, and assign your desired key combination. I’ve set mine to Ctrl+c.

Now, capturing links is as simple as pressing Ctrl+c while browsing in Safari, instantly adding them to your Obsidian reading list.